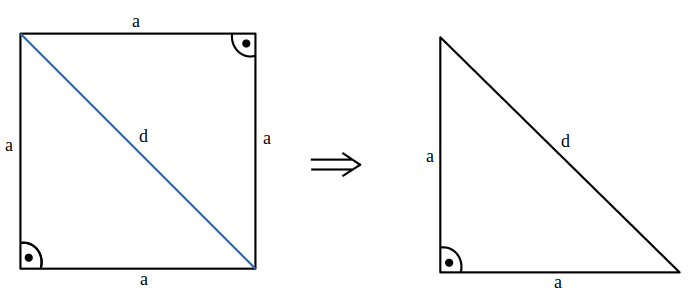
![]()
![]()
![]()
![]()
![]()
![]()
și
![]()
![]()
Exerciții
- Calculează lungimea diagonalei pătratului dacă este dată latura
a)
b)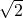
c)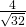
—————————————
Rezolvare:
a)
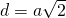
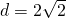
————————————–
b)
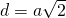
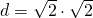
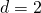
————————————–
c)
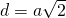
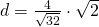
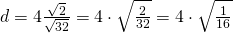
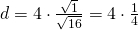
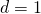
- Calculează perimetrul pătratului dacă diagonala este de:
a)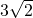
b)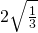
c)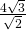
————————————–
Rezolvare:
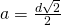
a)
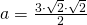
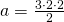
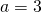
Perimetrul: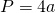
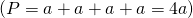
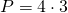
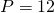
————————————-
b)
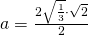
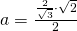
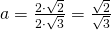
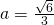
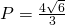
————————————-
c)
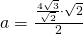
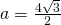
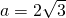
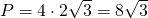
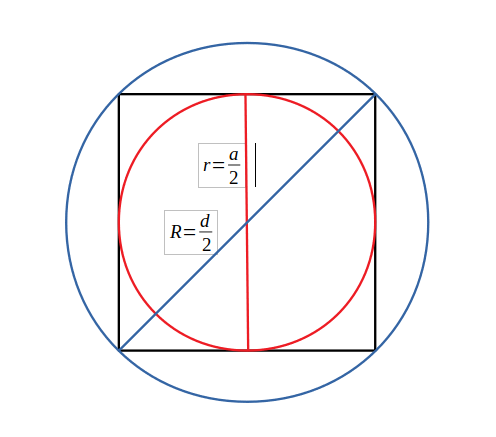
- Calculează raza cercului circumscris și înscris al unui pătrat având diagonala de 8cm
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
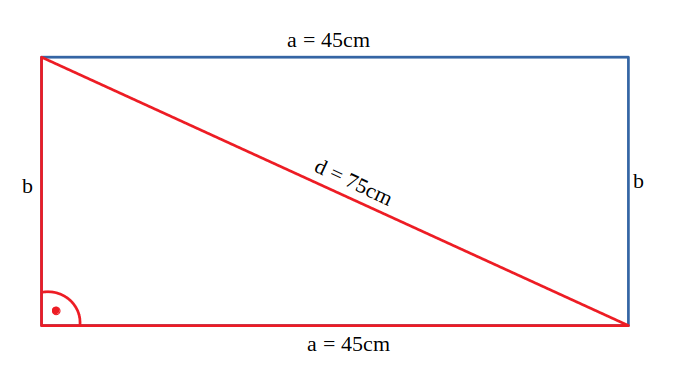
4. Diagonala unui dreptunghi este 75 cm, iar lățimea este 45 cm. Calculează perimetrul dreptunghiului.
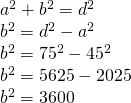
![]()
![]()
![]()
![]()
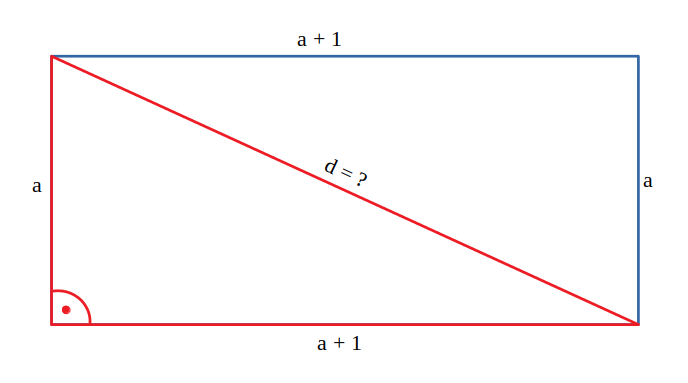
5. Perimetrul dreptunghiului este 14cm, iar o latură este cu 1cm mai mare decât cealaltă latură. Cât este diagonala acestui dreptunghi?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()