Prisma hexagonală – Matematica

noiembrie 6, 2018noiembrie 7, 2018 matishPosted in Uncategorized

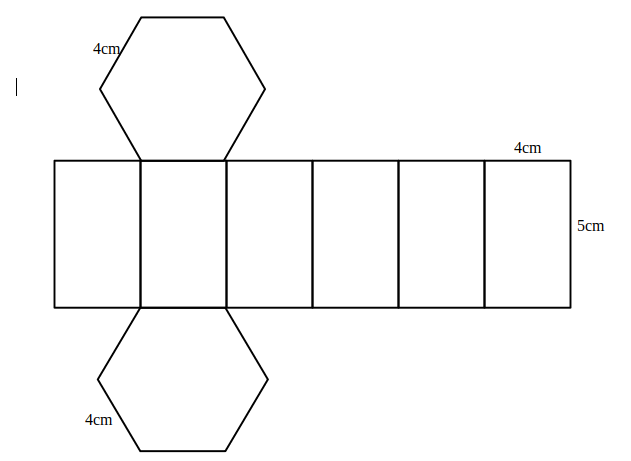
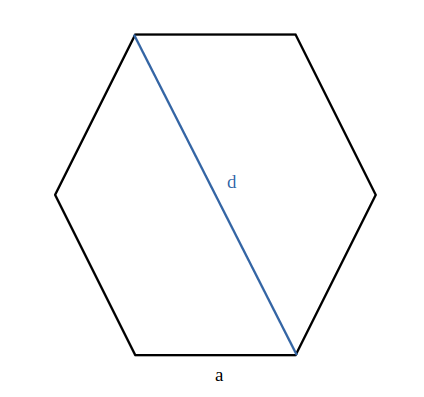
Desenează desfășurarea prismei hexagonale din figură și calculează aria sa.

—–
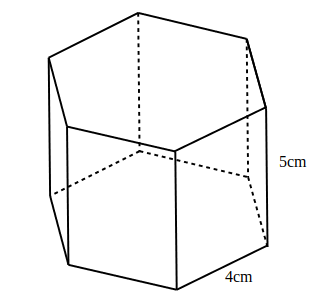
Soluție:

—-
Aria bazei: Un hexagon regulat este format din 6 triunghiuri echilaterale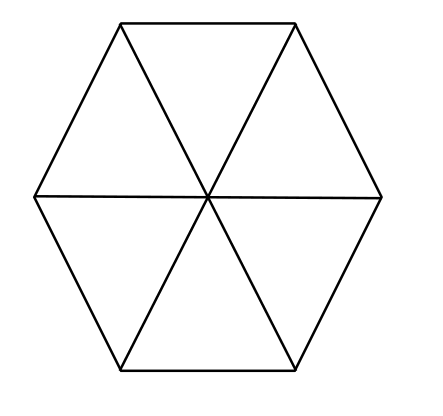
$A_b = 6 \cdot { \frac {a^2 \sqrt{3}} {4}}$
$A_b = { \frac {3a^2 \sqrt{3}} {2}}$
$A_b = \frac { 3 \cdot 16 \cdot \sqrt { 3 } } { 2 }$
—-
$A_b = 24 \sqrt { 3 } cm ^ { 2 }$
—-
$\begin{array} { l } { A_l = 6 a \cdot H } \\ { A_l = 6 \cdot 4 \cdot 5 } \\ { A_l = 120 \operatorname { cm } ^ { 2 } } \end{array}$
—-
$\begin{array} { l } { A = 2 A_b + A_l } \\ { A = 2 \cdot 24 \sqrt { 3 } + 120 } \\ { A = 120 + 48 \sqrt { 3 } } \\ { A = 24 ( 5 + 2 \sqrt { 3 } )cm ^ { 2 } } \end{array}$
—-
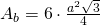
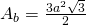
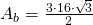
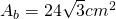
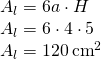
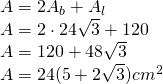
Calculează înălțimea prismei hexagonale regulate dacă este cunoscută aria sa de 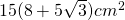$15 ( 8 + 5 \sqrt { 3 } ) cm ^ { 2 }$ și diagonala mai lungă a bazei este 10 cm
—-
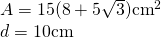
$\begin{array} { l } { A = 15 ( 8 + 5 \sqrt { 3 } ) \mathrm { cm } ^ { 2 } } \\ { d = 10 \mathrm { cm } } \end{array}$
—
H=?
—

$\begin{array} { l } { d = 2 a } \\ { a = \frac { d } { 2 } } \\ { a = 5 cm } \end{array}$
—-
$\begin{array} { l } { A = 2 A_b + A_l } \\ { P = { 2 } \cdot 6 \cdot \frac { a ^ { 2 } \sqrt { 3 } } { 4 } + 6 a \cdot H } \end{array}$
—-
$A = 3 a ^ { 2 } \sqrt { 3 } + 6 a \cdot H = 15 ( 8 + 5 \sqrt { 3 } )$
—
$3 \cdot 25 \sqrt { 3 } + 6 \cdot 5 \cdot H = 15 ( 8 + 5 \sqrt { 3 } )$
—
$15 ( 5 \sqrt { 3 } + 24 ) = 15 ( 8 + 5 \sqrt { 3 } )$
$5 \sqrt { 3 } + 2 H = 8 + 5 \sqrt { 3 }$
—
$H=4cm$
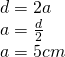
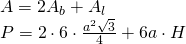
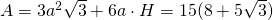
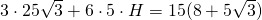
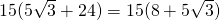
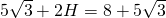
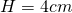
Calculează volumul prismei din figură

$V = A_b \cdot H$
$\begin{array} { l } { A_b = 6 \cdot \frac { a ^ { 2 } \sqrt { 3 } } { 4 } } \\ { A_b = 6 \cdot \frac { 64 \sqrt { 3 } } { 4 } } \end{array}$
$A_b = 96 \sqrt { 3 } \mathrm { cm } ^ { 2 }$
$\begin{array} { l } { V = 96 \sqrt { 3 } \cdot 11 } \\ { V = 1056 \sqrt { 3 } \mathrm { cm } ^ { 3 } } \end{array}$
—
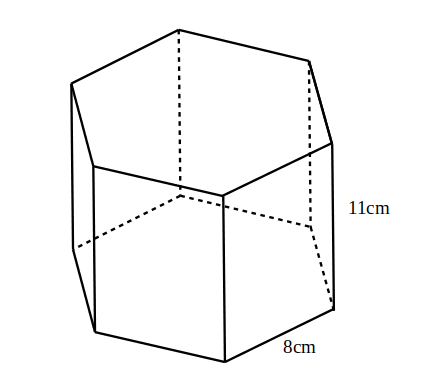
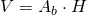
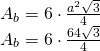
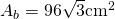
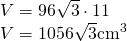
Latura laterală a unei prisme hexagonale regulate cu diagonala cea mai lungă a prismei formează un unghi de 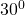$30^0$ . Calculează volumul prismei dacă diagonala mai lungă este 8cm.
—

$\begin{array} { l } { D = 8 \mathrm { cm } } \\ { d = \frac { D } { 2 } } \\ { d = 4 \mathrm { cm } } \end{array}$
—
$\begin{array} { l } { d = 2 a } \\ { a = \frac { d } { 2 } } \\ { a = 2 c m } \end{array}$
—
$\begin{array} { l } { A_b = 6 - \frac { a ^ { 2 } \sqrt { 3 } } { 4 } } \\ { A_b = 6 \cdot \frac { 4 \sqrt { 3 } } { 4 } } \\ { A_b = 6 \sqrt { 3 } cm^2 } \end{array}$
—
$\begin{array} { l } { H ^ { 2 } = D ^ { 2 } - d ^ { 2 } } \\ { H ^ { 2 } = 64 - 16 } \\ { H ^ { 2 } = 48 } \\ { H = \sqrt { 16 \cdot 3 } } \\ { H = 4 \sqrt { 3 } \operatorname { cm } } \end{array}$
—
$\begin{array} { l } { V = A_b \cdot H } \\ { V = 6 \sqrt { 3 } \cdot 4 \sqrt { 3 } } \\ { V = 24 \cdot 3 } \\ { V = 72 \operatorname { cm } ^ { 3 } } \end{array}$
—
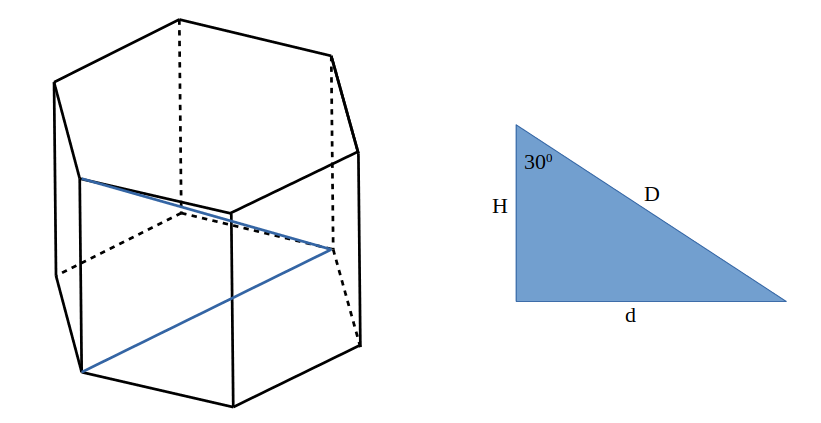
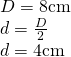
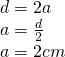
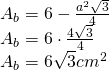
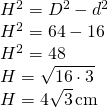
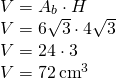
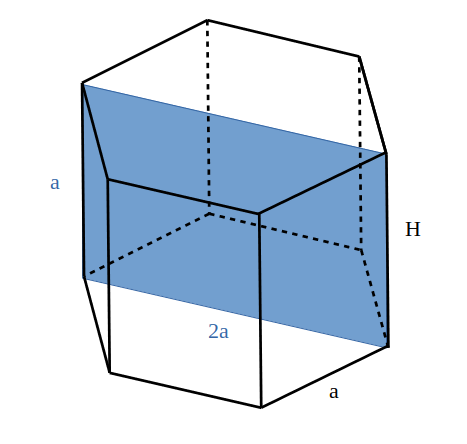
Prisma hexagonală regulată are aria secțiunii diagonale mai mari de 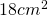$18 cm^2$ . Toate laturile prismei sunt egale. Calculează aria și volumul prismei

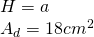
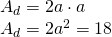
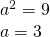
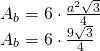
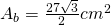
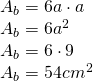
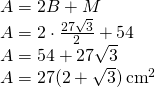
$\begin{array} { l } { H = a } \\ {A _ { d } = 18 cm ^ { 2 } } \end{array}$
—
$\begin{array} { l } { A _ { d } = 2 a \cdot a } \\ { A _ { d } = 2 a ^ { 2 } = 18 } \end{array}$
$\begin{array} { l } { a ^ { 2 } =9 } \\ { a = 3 } \end{array}$
—
$\begin{array} { l } { A_b = 6 \cdot \frac { a ^ { 2 } \sqrt { 3 } } { 4 } } \\ { A_b = 6 \cdot \frac { 9 \sqrt { 3 } } { 4 } } \end{array}$
—
$A_b = \frac { 27 \sqrt { 3 } } { 2 } cm ^ { 2 }$
—
$\begin{array} { l } { A_b = 6 a \cdot a } \\ { A_b = 6 a ^ { 2 } } \\ { A_b = 6 \cdot 9 } \\ { A_b = 54 cm ^ { 2 } } \end{array}$
—
$\begin{array} { l } { A = 2 B + M } \\ { A = 2 \cdot \frac { 27 \sqrt { 3 } } { 2 } + 54 } \\ { A = 54 + 27 \sqrt { 3 } } \\ { A = 27 ( 2 + \sqrt { 3 } ) \operatorname { cm } ^ { 2 } } \end{array}$
—
$\begin{array} { l } { V = A_b \cdot H } \\ { V = \frac { 27 \sqrt { 3 } } { 2 } \cdot 3 } \\ { V = \frac { 81 \sqrt3} { 2 } cm ^ { 3 } } \end{array}$

Lasă un răspuns Anulează răspunsul