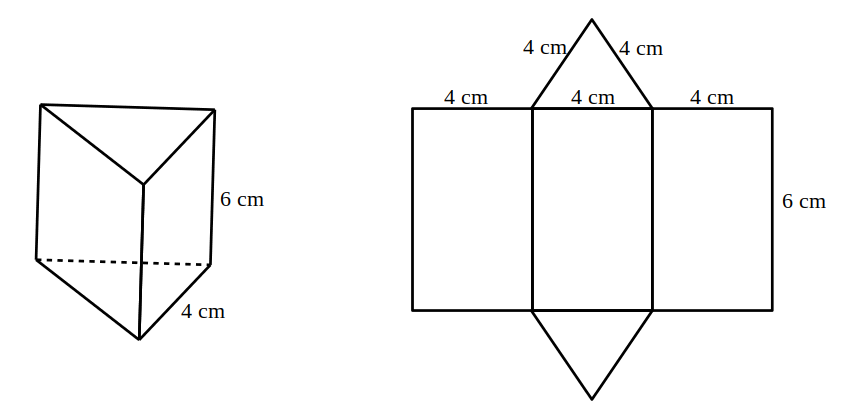
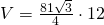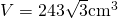- Desenează desfășurarea prismei triunghiulare regulate și calculează aria sa

—
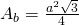
—–
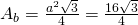

—–

—–
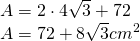
- Calulează latura bazei a unei prisme triunghiulare regulate. A cărei înălțime este dublu mai mare decât latura bazei, iar aria este
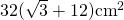
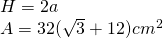
—
a=?
—
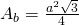
—
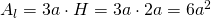
—
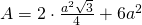
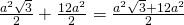
—
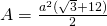
—
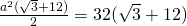
—
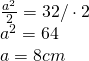
- Calculează volumul prismei regulate din figură

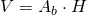
—
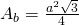
—
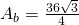
—
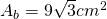
—
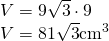
— - Aria laterală a unei prisme triunghiulare regulate, a cărei toate laturile sunt egale, este de
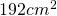 . Calculează volumul prismei.
. Calculează volumul prismei.
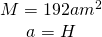
—
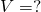
—
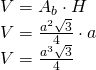
—

—
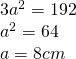
—
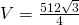
—
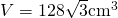
- Latura bazei unei prisme triunghiulare regulate este 9cm. Cât este volumul prismei dacă diagonala feței laterale este 15cm?
—-

—
—
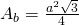
—

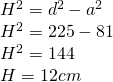
—
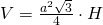
—