Punctul, dreapta, planul

Dreapta este definită cu două puncte diferite. Pentru două puncte diferite există o dreaptă care conține aceste puncte.

Punctele care aparțin unei drepte sunt coliniare. Punctele necoliniare nu pot aparține unei drepte.

Planul este definit de minim 3 puncte necoliniare.

Punctele care aparțin unui plan sunt coplanare. Punctele care nu pot aparține aceluiași plan sunt necoplanare.

Exerciții:

1. Sunt date punctele precum în figurile de mai jos. Câte drepte pot defini aceste puncte?
   
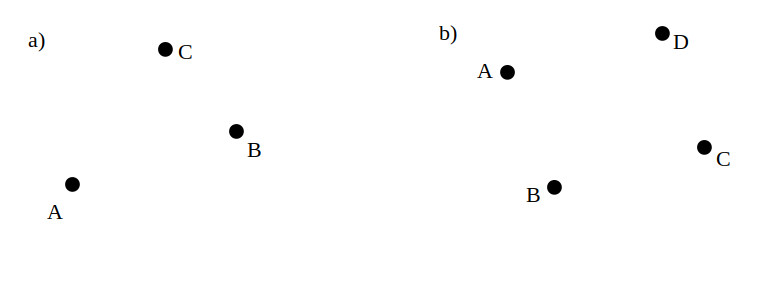
2. Sunt date punctele A, B, C și D. Câte drepte există care:
   a) Conțin punctul A
   b) Conțin punctul A și B
   c) Conțin trei puncte A, B și C
   d) Punctul D și încă un punct din punctele A, B, C
   e) Punctele B, C și încă un punct dintre punctele A și D
3. Pe dreapta a sunt date punctele K, L, M, N, P. Punctul Q este în afara dreptei a. Câte drepte pot trece prin punctul Q, astfel încât fiecare dreaptă să conțină una din punctele K, L, M, N, P? Dacă și punctul R este în afara dreptei a, câte drepte pot defini punctele K, L, M, N, P, Q, R?
4. Dacă planul 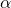este planul care este în fața cuboidului din figură. Este evident că 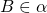și 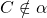. Folosind semnele  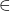și 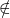 notează relația fiecărui vârf cu planul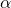 
   
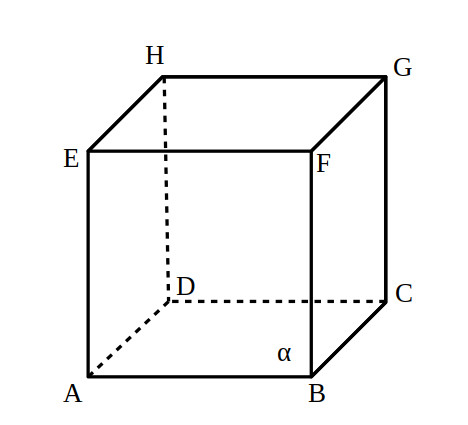
5. Definește toate dreptele care conțin punctul A al cuboidului, câteva perechi de drepte perpendiculare, drepte paralele, plane paralele și plane perpendiculare.