Exerciții
- a)
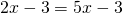 (Soluție)
(Soluție)
——————————————————————
Rezolvare:
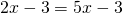
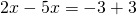
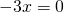
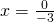
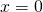
——————————————————————
b)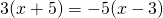 (Soluție)
(Soluție)
c)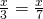 (Soluție)
(Soluție)
d)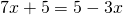 (Soluție)
(Soluție)
e)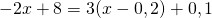 (Soluție)
(Soluție)
f)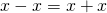 (Soluție)
(Soluție)
g)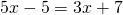 (Soluție)
(Soluție)
h)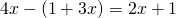 (Soluție)
(Soluție) - a)
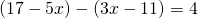 (Soluție)
(Soluție)
——————————————————————
Rezolvare:
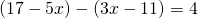
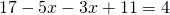 (eliberare de paranteze)
(eliberare de paranteze)
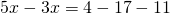
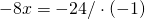
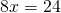
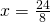
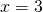
——————————————————————-
b)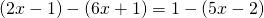 (Soluție)
(Soluție)
c)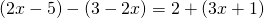 (Soluție)
(Soluție)
d)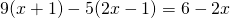 (Soluție)
(Soluție)
e)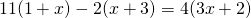 (Soluție)
(Soluție)
f)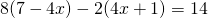 (Soluție)
(Soluție)
g)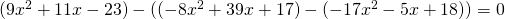 (Soluție)
(Soluție) - a)
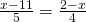 (Soluție)
(Soluție)
————————————————————————————————–
Rezolvare:
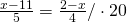 (simplificarea fractiei)
(simplificarea fractiei)
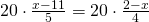
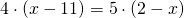
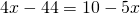
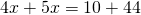
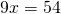
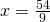
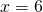
—————————————————————————————————-
b)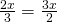 (Soluție)
(Soluție)
c)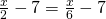 (Soluție)
(Soluție)
d)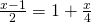 (Soluție)
(Soluție)
e)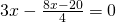 (Soluție)
(Soluție)
f)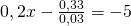 (Soluție)
(Soluție)
g)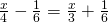 (Soluție)
(Soluție)
h)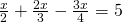 (Soluție)
(Soluție)
i)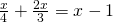 (Soluție)
(Soluție)
j)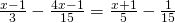 (Soluție)
(Soluție)
k)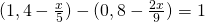 (Soluție)
(Soluție)
l)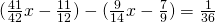 (Soluție)
(Soluție)
m)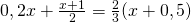 (Soluție)
(Soluție) - a)
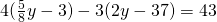 (Soluție)
(Soluție)
———————————————————————————–
Rezolvare:
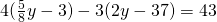
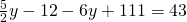
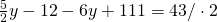
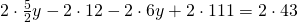
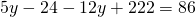
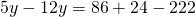
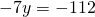
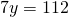
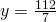
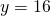
————————————————————————————
b)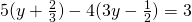 (Soluție)
(Soluție)
c)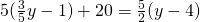 (Soluție)
(Soluție)
d)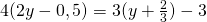 (Soluție)
(Soluție)
e)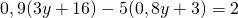 (Soluție)
(Soluție)
f)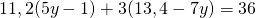 (Soluție)
(Soluție)
g)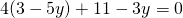 (Soluție)
(Soluție)
h)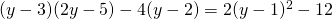 (Soluție)
(Soluție) - a)
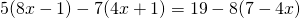 (Soluție)
(Soluție)
—————————————————————————–
Rezolvare:
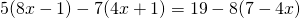
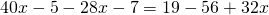
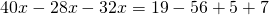
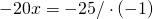
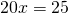
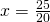
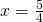
—————————————————————————–
b)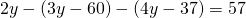 (Soluție)
(Soluție)
c)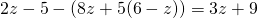 (Soluție)
(Soluție)
d)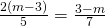 (Soluție)
(Soluție)
e)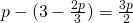 (Soluție)
(Soluție)
f)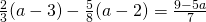 (Soluție)
(Soluție)
g)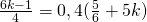 (Soluție)
(Soluție)
h)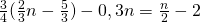 (Soluție)
(Soluție)
i)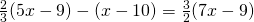 (Soluție)
(Soluție)
j)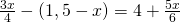 (Soluție)
(Soluție) - a)
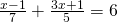 (Soluție)
(Soluție)
—————————————————————————–
Rezolvare:
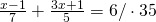
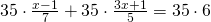
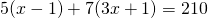
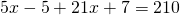
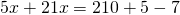
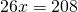
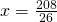
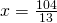
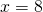
—————————————————————————–
b)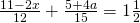 (Soluție)
(Soluție)
c)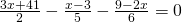 (Soluție)
(Soluție)
d)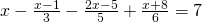 (Soluție)
(Soluție)
e)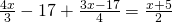 (Soluție)
(Soluție)
f)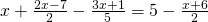 (Soluție)
(Soluție)
g)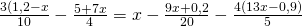 (Soluție)
(Soluție)
h)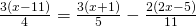 (Soluție)
(Soluție)
i)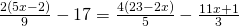 (Soluție)
(Soluție)
j)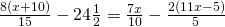 (Soluție)
(Soluție) - a)
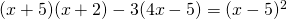 (Soluție)
(Soluție)
—————————————————————
Rezolvare:
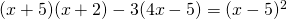
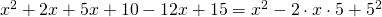
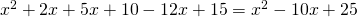
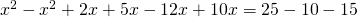
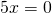
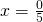
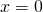
—————————————————————
b)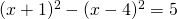 (Soluție)
(Soluție)
c)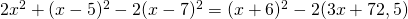 (Soluție)
(Soluție)
d)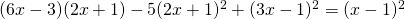 (Soluție)
(Soluție)
e)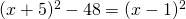 (Soluție)
(Soluție)
f)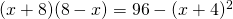 (Soluție)
(Soluție)
g)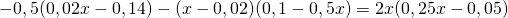 (Soluție)
(Soluție)
h)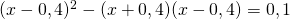 (Soluție)
(Soluție)
i)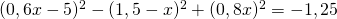 (Soluție)
(Soluție)
j)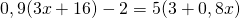 (Soluție)
(Soluție)
k)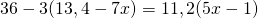 (Soluție)
(Soluție) - a)
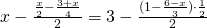 (Soluție)
(Soluție)
b)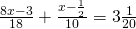 (Soluție)
(Soluție)
c)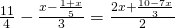 (Soluție)
(Soluție)