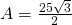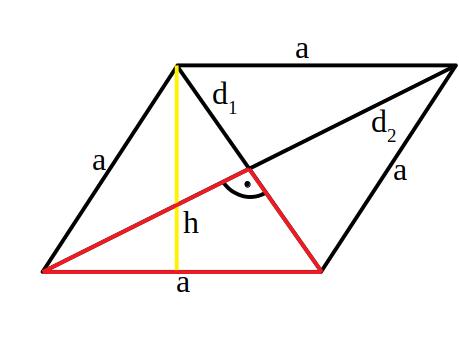
![]()
![]()
![]()
![]()
Exerciții
- Calculează perimetrul și înălțimea rombului dacă sunt cunoscute diagonalele sale:
a)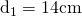 și
și 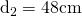
b)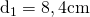 și
și 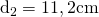
———
Rezolvare
a)
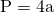
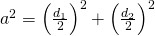
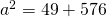
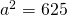
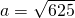
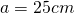
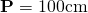
—
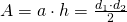
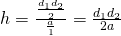
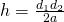
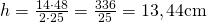
—————————————————-
b)
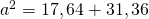
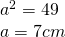
—
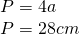
—
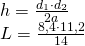
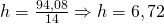 cm
cm - Aria rombului este de 96
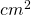 , lungimea unei diagonale este de 16 cm. Calculeaza perimetrul rombului.
, lungimea unei diagonale este de 16 cm. Calculeaza perimetrul rombului.
———————–
Rezolvare
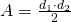
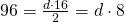
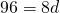
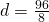
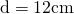
—
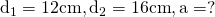
—
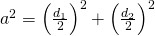
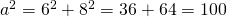
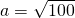
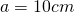
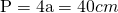
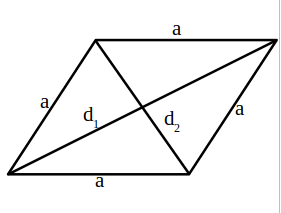
- Prin aplicarea teoremei lui Pitagora la romb dovedește că:
a)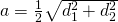
b)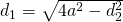
c)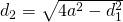
—————————————————
Rezolvare:
a)
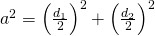
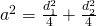
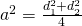
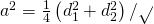
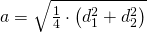
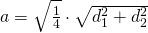
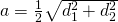
—————–
b)
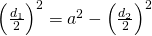
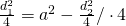
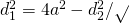
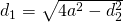
—————–
c)
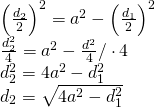
- O diagonală este egală cu lungimea laturii rombului. Calculează cealaltă diagonală
———————————————————
Rezolvare
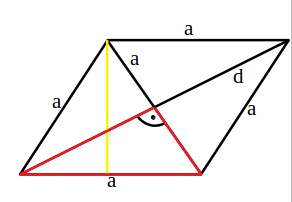
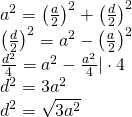
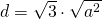
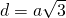
——————————————————– - Unghiul dintre înălțime și diagonala mai scurtă este de
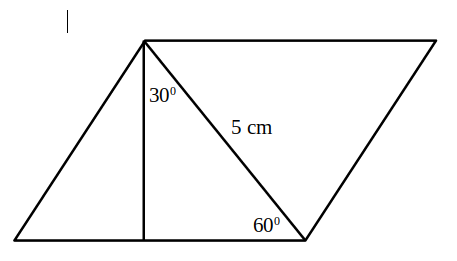
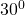 . Dacă lungimea diagonalei mai scurte este 5cm, calculează aria și perimetrul rombului.
. Dacă lungimea diagonalei mai scurte este 5cm, calculează aria și perimetrul rombului.
——————————————————–
Rezolvare
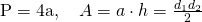
—
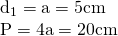
—
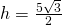
—