
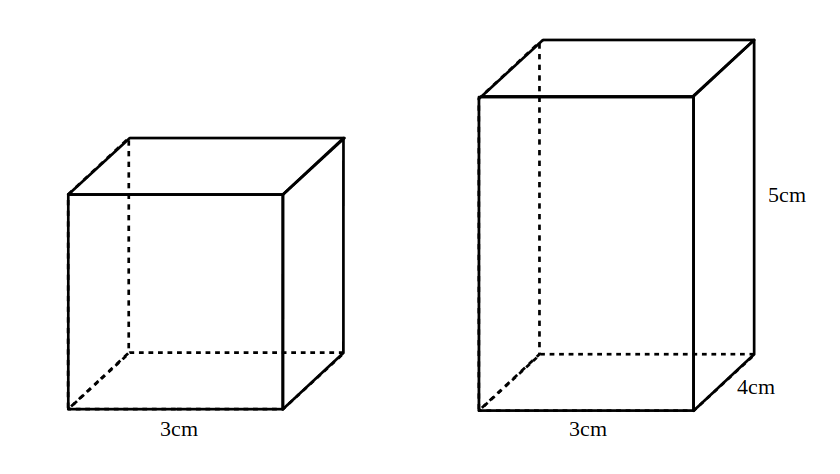
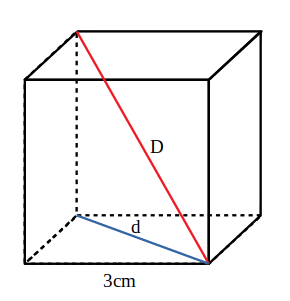
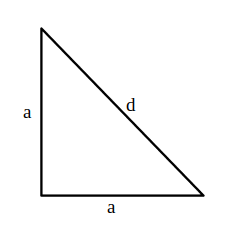
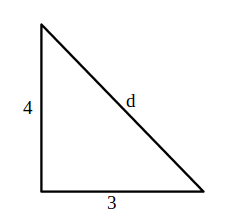
- Calculează diagonala cubului și prismei patrulatere din figură.
——
Soluție
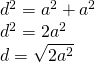
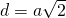
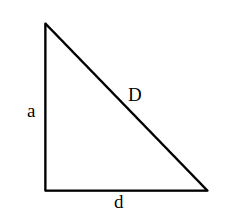
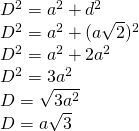
—
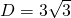
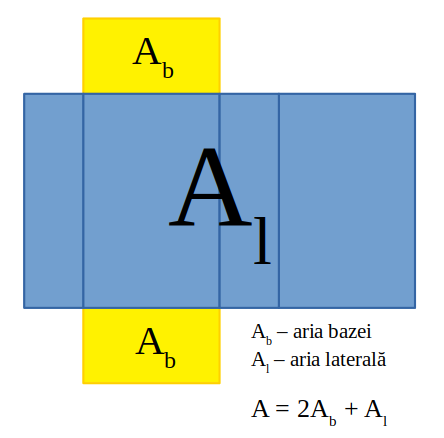
———————————————————————————-
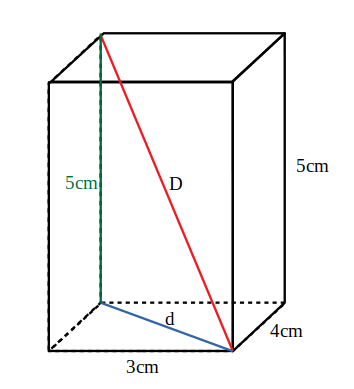
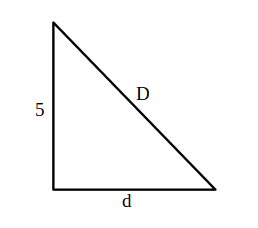
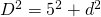
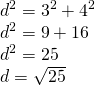
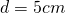
——
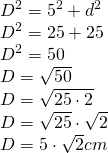
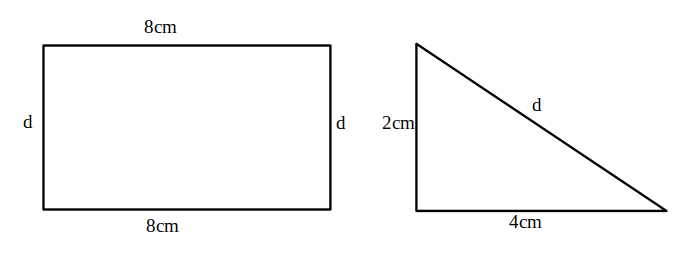
————————— - Calculează aria secțiunii diagonale a prismelor din figuri
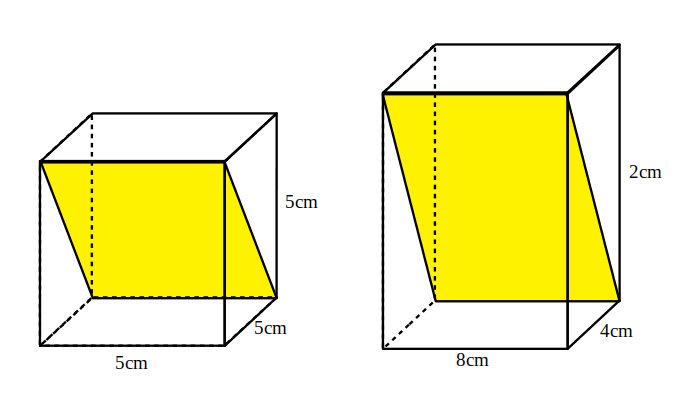
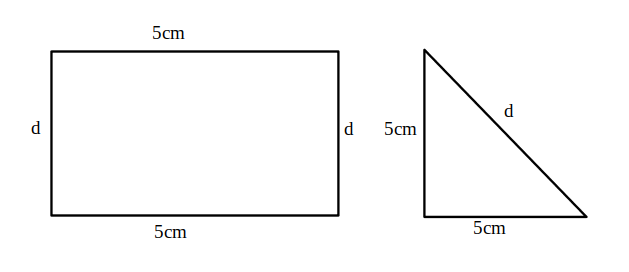
Soluție
—————————
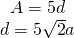
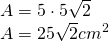
————————–
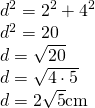
—-
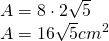
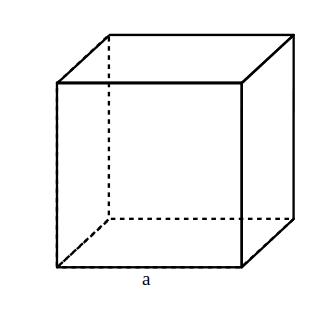
—————————————————— - Latura unui cub este de 4 cm. Desenează desfășurarea cubului și calculează aria sa.
————————-
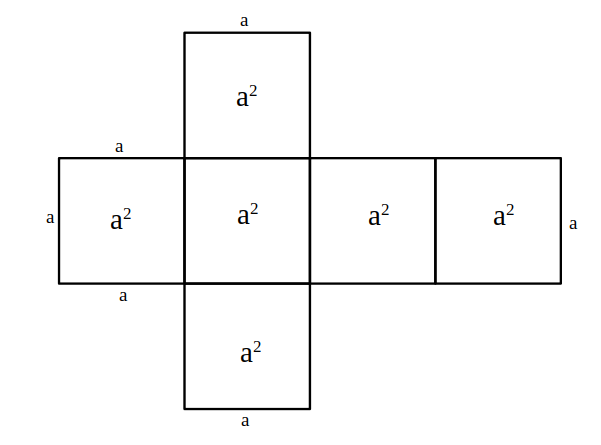
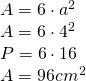
————————- - Desenează desfășurarea prismei din figură și calculează aria sa
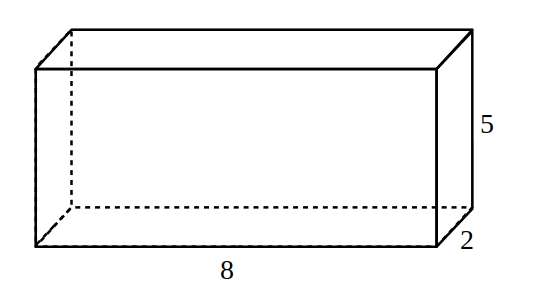
————————————
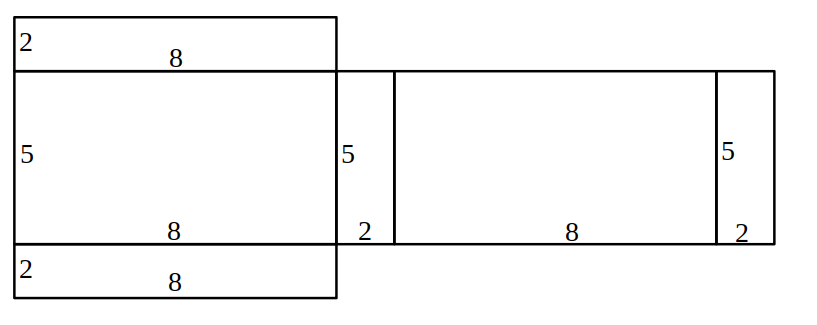
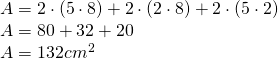 ————————————
———————————— - Latura la bază a unei prisme patrulatere regulate este 40cm. Înălțimea prismei este 60cm. Calculează diagonala și aria prismei
—————————–
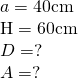
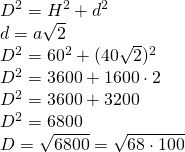
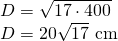

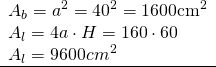
—–
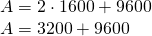
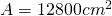
——- - Calculează volumul unui cub a cărui:
a) latură este 2cm
b) diagonala feței este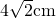
c) diagonala prismei este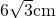
d) aria secțiunii diagonale este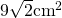
——————
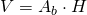
——————
a)
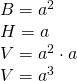
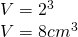
——————
b) - Calculează diagonala prismei și volumul a unei prisme patrulatere care are laturile la bază 5cm și 3cm și înălțimea 4cm.
a = 5cm
b = 3cm
H = 4cm
————————–
Soluție
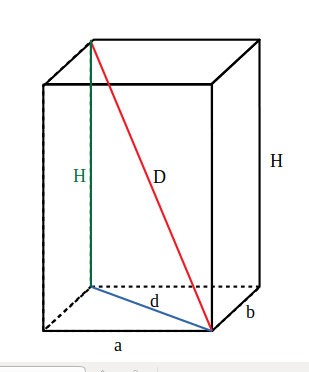
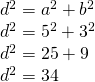
—
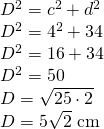
—
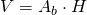
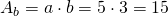
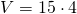
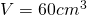
————————– - Calculează volumul prismei patrulatere regulate a cărei înălțime este de 1,5m iar aria laterală este
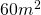
————–
Soluție:
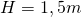
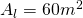
V=?
—
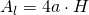
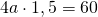
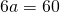
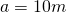
—-
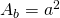
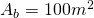
—
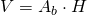
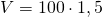
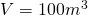
—————————– - Câtă tablă de aluminiu trebuie cumpărată pentru confecționarea unui rezervor de 4500 l dacă baza rezervorului este un pătrat cu latura de 150cm?
Soluție
——–
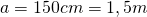
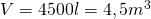
A=?
——–
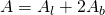
——–
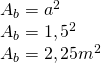
——–
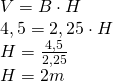
——–
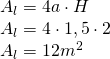
——–
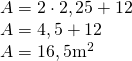
——–
Este necesar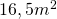 de tablă
de tablă
——–