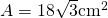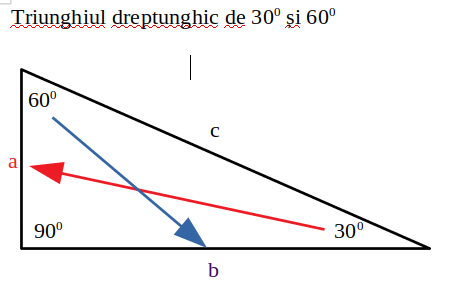
![]()
![]()
Triunghiul isoscel
![]()
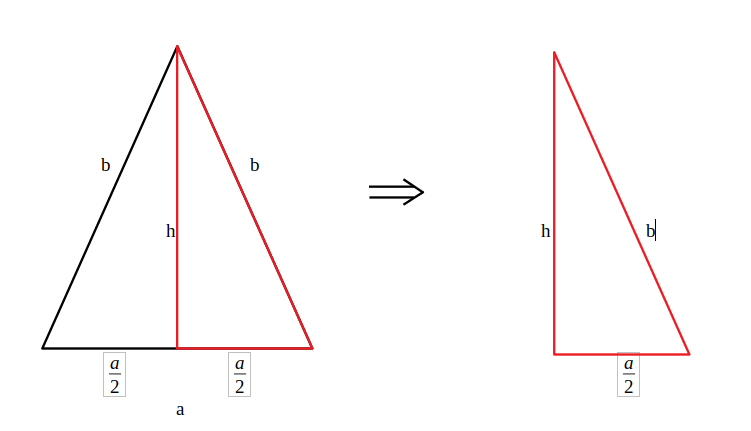
Triunghi echilateral

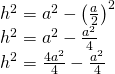
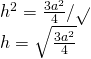
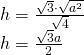
![]()
![]()
![]()
![]()
![]()
![]()
Exerciții
- Calculează necunoscutele din figură

————————————————-
Rezolvare:
a)
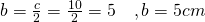
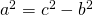
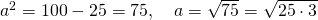
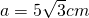
sau
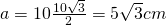
————————————————–
b)
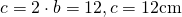
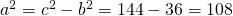
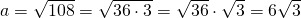
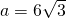
————————————————- - Calculează înălțimea unui triunghi isoscel având baza a și latura b dacă:
a) a = 6cm și b = 5cm
b) a = 16cm și b = 10cm
————————————————-
Rezolvare
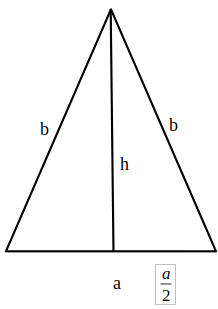
a)
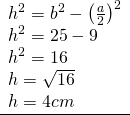
—————————————————-
b)
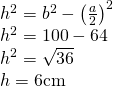
—————————————————- - Cât este aria unui triunghi isoscel dacă baza sa este de 10cm și latura de 13cm?
————————
Rezolvare:
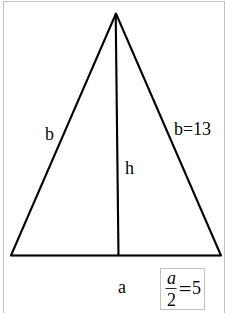
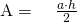
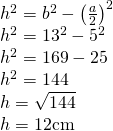
——————————————– - Calculează perimetrul triunghiului isoscel, dacă
a) b = 10cm și ha = 8cm
b) b = 13cm și ha = 5cm
——————————————-
Rezolvare:
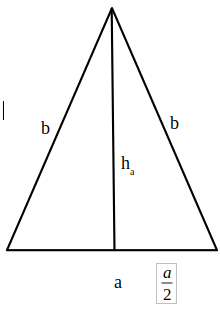
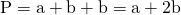
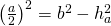
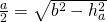
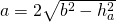
—-
a)
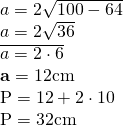
——————————————–
b)
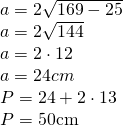
——————————————– - Calculează laturile triunghiului echilateral dacă înălțimea sa este de
a) 4cm
b) 12 dm
——————————————–
Rezolvare:
a)
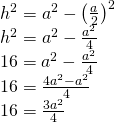
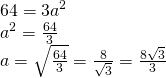
——————————————–
b)
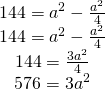
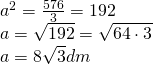
——————————————— - Calculează latura triunghiului echilateral, dacă aria sa este
a)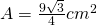
b)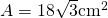
———————————————
Rezolvare:
a)
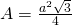
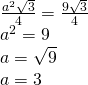
———————————————
b)
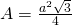
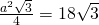
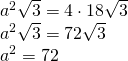
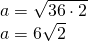
Temă de casă
- Determină laturile necunoscute a figurilor de mai jos
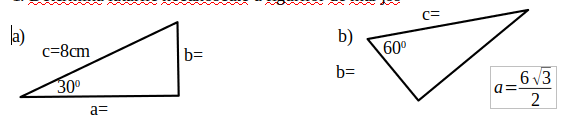
- Calculează înălțimea unui triunghi isoscel care are baza a și laturile egale b, dacă a = 16 cm și b = 10 cm
- Cât este aria unui triunghi isoscel, dacă baza este de 6 cm și latura egală de 5cm?
- Calculează perimetrul triunghiului isoscel, dacă
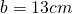 și
și 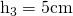
- Calculează laturile triunghiului echilateral dacă înălțimea sa este de 12 dm
- Calculează latura triunghiului echilateral, dacă aria sa este