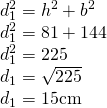Trapez isoscel
![]()
![]()
![]()
![]()
![]()
![]()
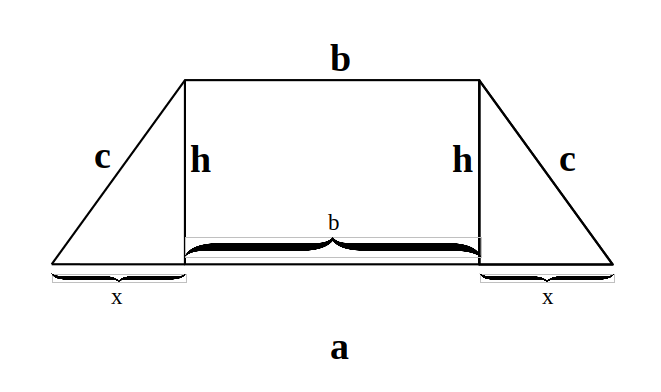
- Calculează perimetrul și aria trapezului isoscel dacă baza mare, latura și înălțimea sunt:
a) a = 28cm, c=25cm și h= 24cm
b) a=15cm, c=9cm și h=7cm
——————————-
Rezolvare:
a)
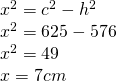
—
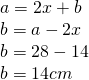
—
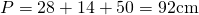
—
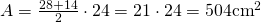
—————————–
b)
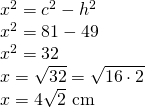
—
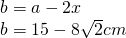
—
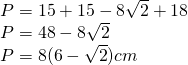
—
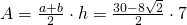
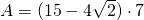
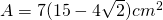
———————— - La un trapez isoscel baza mare este 15cm iar baza mică este 9cm. Unghiul la o bază este de
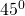 . Calculează aria trapezului
. Calculează aria trapezului
————————
Rezolvare
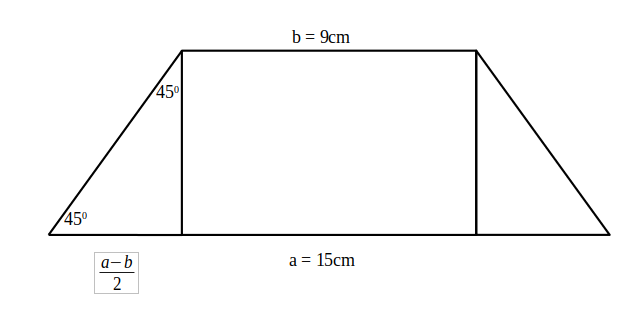
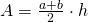
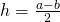
—
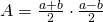
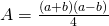
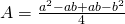
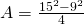
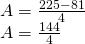
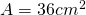
- Perimetrul unui trapez isoscel este 60cm. Dacă bazele sunt de 22cm și 12cm, calculează aria trapezului.
—————————————
Rezolvare
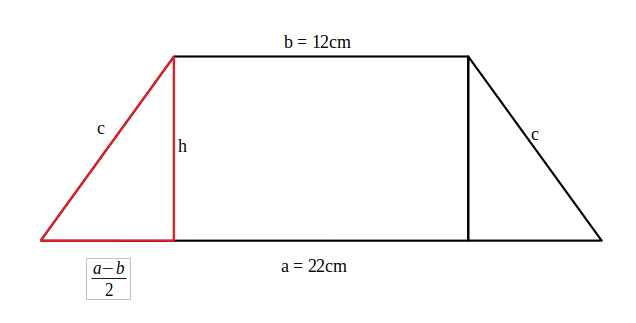
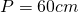
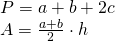
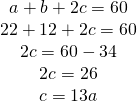
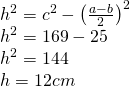
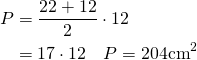
—————————- - Folosind aplicarea teoremei lui Pitagora la trapez demonstrează:
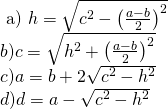
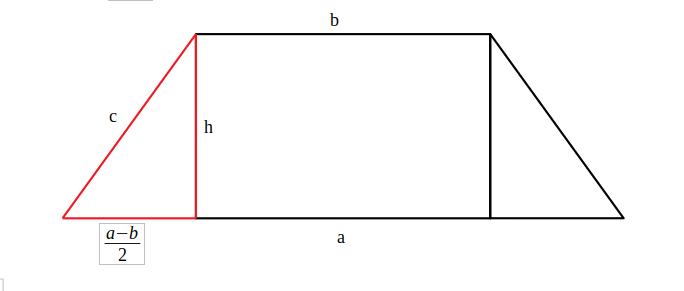
————————————————–
Rezolvare
a)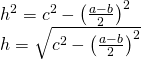
————————————————–
b)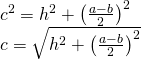
————————————————–
c)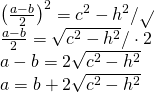
————————————————–
d)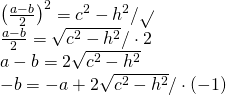
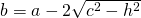
- Calculează perimetrul și aria trapezului dreptunghic la care baza mică este 5cm, înălțimea 12cm și latura 13cm.
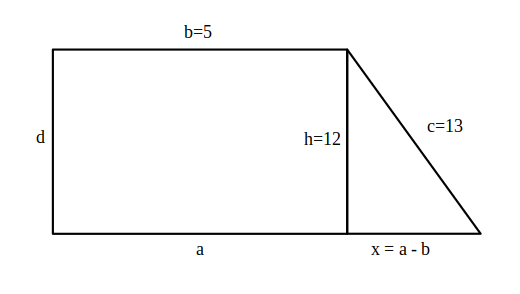
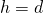
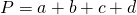
—
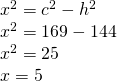
—
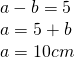
—
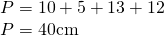
—
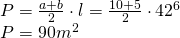
——————————————————— - Calculează diagonalele trapezului dreptunghic care are aria de
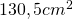 și lungimea bazelor de
și lungimea bazelor de 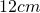 și
și 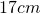
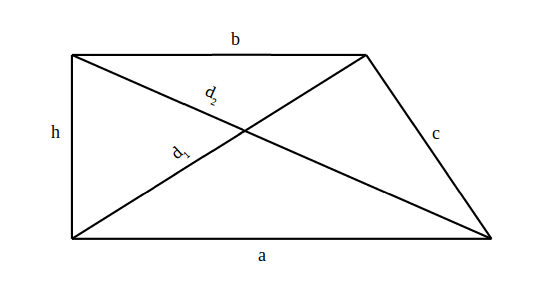
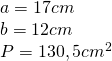
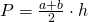
—-
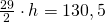
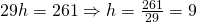
—-
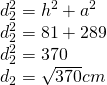
—-